library(statnet)
library(intergraph)
library(igraph)
library(ggraph)
library(graphlayouts)
library(networkdata)
library(tidyverse)17 Exponential Random Graph Models (ERGMs)
So far, the models we’ve considered have treated tie formation as mostly random or locally constrained: ties are formed with fixed probabilities (\(G(n, p)\)), rewired at random (small-world), or arranged to match node degrees (configuration model). However, real-world networks are shaped by richer and more structured processes. People don’t form ties independently or at random, they’re influenced by patterns like mutual friendships, popularity, shared group membership, and social norms like reciprocity and transitivity. For example, two people who share a common friend may be more likely to form a tie themselves (triadic closure), or individuals may be more likely to reciprocate a connection that is initiated by someone else. These kinds of dependencies are central to many social theories, and they give rise to complex patterns of self-organization in networks.
To capture these processes, we need a more flexible modeling framework—one that allows for:
- Multiple network features to be modeled simultaneously
- Direct specification of tie dependencies
- Testing of competing social mechanisms
This leads us to models that are built around network configurations, i.e. small, interpretable patterns of ties (such as mutual ties, stars, and triangles) that collectively describe the structure of the network. These configurations are often nested, meaning they build on one another hierarchically, and they can represent competing explanations for the observed structure. For instance, both reciprocity and popularity could explain why a node has many incoming tie, but these explanations imply different underlying processes.
Exponential Random Graph Models (ERGMs) provide a flexible way to model these kinds of patterns. Instead of assuming each edge forms independently, ERGMs allow the probability of a tie to depend on what else is happening in the network. For example, the likelihood of a tie forming between two nodes may increase if they share mutual connections (triadic closure), or decrease if one node is already connected to many others (crowding out).
By explicitly modeling such configurations, we gain not only better empirical fit but also the ability to test theoretical hypotheses about the generative processes that shape real-world networks.
17.1 Packages Needed for this Chapter
17.2 ERGM Modeling Outline
Exponential Random Graph Models (ERGMs) are a powerful family of statistical models for analyzing and simulating social networks. Unlike simpler random graph models, ERGMs are designed to capture the complex dependencies that often characterize real-world networks, such as reciprocity, transitivity, or clustering—by explicitly modeling how the presence of one tie can affect the likelihood of others.
The core idea is as follows. ERGMs specify a probability distribution over the set of all possible networks with a given number of nodes. The probability of observing a particular graph \(G\) is defined as:
\[ P(G) = \frac{1}{\kappa} \exp\left( \sum_{i=1}^{p} \theta_i \cdot s_i(G) \right) \] where
- \(s_i(G)\) is a network statistic that counts a specific configuration (e.g., number of edges, mutual ties, triangles).
- \(\theta_i\) is the parameter associated with statistic \(s_i(G)\); it tells us how strongly that configuration influences tie formation.
- \(\kappa\) is a normalizing constant ensuring that all possible graphs sum to a probability of 1: \[ \kappa = \sum_{G'} \exp\left( \sum_{i=1}^{p} \theta_i \cdot s_i(G') \right) \]
This formulation makes clear that networks with more of the structures positively weighted by \(\theta\) are more probable. For instance, a large positive \(\theta_{\text{mutual}}\) implies that the observed network contains more reciprocated ties than expected by chance.
In general, we interpret the parameters as follows:
- A positive \(\theta_i\) means that the corresponding configuration (e.g., triangles) is overrepresented in the observed network than what is expected by pure chance.
- A negative \(\theta_i\) indicates that the configuration is underrepresented than what is expected by pure chance.
- A zero value implies that the configuration occurs at chance levels.
The statistics \(s_i\) are network configurations. As mentioned, ERGMs rely on small, interpretable network configurations to explain structure. These include:
- Edges: baseline tendency for tie formation (controls overall density)
- Mutual: reciprocity in directed networks
- Triangles: clustering or transitivity (friends of friends)
- Stars: centralization or popularity (many ties to a node)
- Homophily: ties between nodes with similar attributes
Each of these configurations reflects a hypothesized mechanism that may drive the evolution of network structure. We formalize some of the standard statistics in the following.
In the following section, we will move through four generations of dependence assumptions yielding different ERGM specifications with statistics (network configurations) that are included in the model.
Specifying an ERGM in R
An ERGM is specified using a formula that defines the network structure and any covariates to be included. The ergm() function takes a network object on the left-hand side and a set of model terms on the right-hand side.
Here is an example model including edge density, a node-level covariate, homophily on an attribute, and a structural dependency term (gwesp):
ergm(network_object ~ model_terms)where model_terms represent structural configurations or covariate effects, e.g., edges, triangles, mutual, etc. For a full list of available statistics in the ergm package you can check:
?ergmTerm17.2.1 Model Specification
1. Dyadic Independence: Edges and Homophily
To begin working with exponential random graph models (ERGMs), we first need to understand how models are specified and what kinds of network structures they describe. In this section, we introduce the simplest possible ERGM, one that assumes Bernoulli dependence, and show how it connects to the familiar \(G(n, p)\) model. This first step lays the foundation for more complex ERGMs that incorporate structural dependencies.
The Bernoulli ERGM assumes that all possible edges form independently of one another. In other words, the probability that a tie exists between nodes \(u\) and \(v\) is unrelated to whether other ties are present elsewhere in the network. This is a very strong assumption—and one that is often unrealistic in practice—but it is useful as a baseline.
Let \(Y_{uv}\) be a binary random variable indicating the presence (\(1\)) or absence (\(0\)) of a tie between nodes \(u\) and \(v\). The full graph \(G\) can then be represented by its adjacency matrix \(Y\), where \(Y_{uv}\) encodes the tie between \(u\) and \(v\).
In the general formulation of an exponential random graph model, one could imagine assigning a different parameter \(\theta_{uv}\) to every possible tie \((u, v)\) in the network. This would allow the model to express highly specific tendencies for each dyad. The probability of observing a network \(G\) under this formulation would be:
\[ P(G) = \frac{1}{\kappa} \exp\left( \sum_{u<v} \theta_{uv} y_{uv} \right) \]
However, this model quickly becomes infeasible because it would require estimating a separate parameter for every possible edge—a number that grows quadratically with the number of nodes.
To make the model estimable and interpretable, ERGMs rely on the homogeneity assumption: the effect of a given configuration (such as an edge, triangle, or mutual tie) is the same wherever it appears in the network. That is, all instances of the same configuration share a single global parameter. For the Bernoulli ERGM, this means:
\[ \theta_{uv} = \theta \quad \text{for all } (u, v) \]
Applying this assumption simplifies the model considerably:
\[ P(G) = \frac{1}{\kappa} \exp\left( \theta \sum_{u<v} y_{uv} \right) = \frac{1}{\kappa} \exp(\theta \cdot L) \]
Here, \(L\) is the total number of edges in the network, \(\theta\) is a single parameter that governs the overall probability of tie formation, and \(\kappa\) is the normalizing constant ensuring all probabilities sum to 1.
This structure implies that each potential tie forms independently with the same probability, much like in a \(G(n, p)\) random graph. Here, the parameter \(\theta\) governs the log-odds of a tie between any two nodes. More formally, the relationship between \(\theta\) and the tie probability \(p\) (i.e., the density of the network) is:
\[ \theta = \log\left( \frac{p}{1 - p} \right) \quad \Leftrightarrow \quad p = \frac{e^\theta}{1 + e^\theta} \]
This means that:
- When \(\theta = 0\), the expected density is \(p\) = 0.5
- When \(\theta < 0\), the expected density is less than 0.5 (a sparse network)
- When \(\theta > 0\), the expected density is greater than 0.5
So, the edge parameter directly controls the overall density of the network. In practice, real-world social networks tend to be sparse, so \(\theta\) is typically negative. This relationship also means that if you estimate a Bernoulli ERGM and obtain an edge coefficient \(\hat{\theta}\), you can compute the implied expected density using:
\[ \hat{p} = \frac{e^{\hat{\theta}}}{1 + e^{\hat{\theta}}} \]
This makes the edge parameter easy to interpret: it is just the logit-transformed density.
Note: \(G(n, p)\) as a Special Case of ERGM
The Bernoulli ERGM is structurally identical to the \(G(n, p)\) model, with the relationship:
- \(\theta = 0\) → expected density \(p = 0.5\)
- \(\theta > 0\) → expected density \(p > 0.5\)
- \(\theta < 0\) → expected density \(p < 0.5\)
However, this does not hold in general (if the ERGM contains other statistics).
Put differently, the \(G(n, p)\) random graph model is actually a special case of an ERGM. It includes only one term: the number of edges.
In ERGMs, a parameter estimate is considered statistically significant (by convention) if the absolute value of the estimate is greater than approximately twice its standard error (i.e., \(|\hat{\theta}| > 2 \cdot \text{SE}\)). This rule of thumb suggests that the corresponding network feature (such as homophily or reciprocity) is unlikely to have arisen by chance, and is therefore meaningfully associated with the observed pattern of tie formation.
Example: Coleman Friendship
To demonstrate the Bernoulli ERGM, we fit the model to the Coleman high school friendship network used in Chapter 15. However, here we convert ther graph object into an adjacency matrix since the ergm response argument needs to be a network object or a matrix that can be coerced to a network object.
# Load data as graph object from networkdata and extract the fall network
coleman_g <- networkdata::coleman[[1]]
# Convert to adjacency matrix
coleman_mat <- as_adjacency_matrix(coleman_g, sparse = FALSE)
# Fit Bernoulli ERGM with only the edge term
model_bern <- ergm(coleman_mat ~ edges)
summary(model_bern)Call:
ergm(formula = coleman_mat ~ edges)
Maximum Likelihood Results:
Estimate Std. Error MCMC % z value Pr(>|z|)
edges -3.02673 0.06569 0 -46.08 <1e-04 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Null Deviance: 7286 on 5256 degrees of freedom
Residual Deviance: 1969 on 5255 degrees of freedom
AIC: 1971 BIC: 1977 (Smaller is better. MC Std. Err. = 0)The output provides the estimated \(\theta\) parameter for the edge term. A strongly negative value suggests that the probability of a tie between any two students is low, which is typical of real-world social networks that are sparse.
The estimated edge parameter from the Bernoulli ERGM is: \[ \hat{\theta}_{\text{edges}} = -3.02673 \]
This value reflects the log-odds of a tie forming between any two nodes in the network. To convert this into an expected tie probability (i.e., network density), we apply the inverse logit function:
\[ p = \frac{e^{\hat{\theta}}}{1 + e^{\hat{\theta}}} \]
Substituting the estimated value:
\[ p = \frac{e^{-3.02673}}{1 + e^{-3.02673}} \approx 0.046 \]
This result implies that the expected density of the network under this model is approximately 4.6%. This is in fact the density of the observed network which you can verify:
edge_density(coleman_g)[1] 0.04623288Another class of network statistics in ERGMs captures homophily: the tendency of individuals to form ties with others who are similar to themselves in a particular attribute, such as gender, age, race, or occupation.
Let each node in the network have a categorical attribute, denoted:
\[ a : V \rightarrow \{1, \dots, c\} \]
This maps each actor to one of \(c\) categories. To model homophily, we define a statistic that counts the number of ties between actors who share the same attribute value:
\[ m_a(G) = \left| \left\{ \{u, v\} \in E : a(u) = a(v) \right\} \right| \]
That is, \(m_a(G)\) is the number of edges where both endpoints belong to the same category. Adding this statistic to the ERGM, the model becomes:
\[ P(G) = \frac{1}{\kappa} \exp\left( \theta_1 \cdot L + \theta_2 \cdot m_a(G) \right) \]
We interpret the homophily parameter as follows:
- \(\theta_2 > 0\): Ties between similar nodes are more likely (homophily)
- \(\theta_2 < 0\): Ties between dissimilar nodes are more likely (heterophily)
- \(\theta_2 = 0\): No effect of similarity
This formulation assumes that the tendency for similarity-based tie formation is uniform across all dyads, consistent with the homogeneity assumption discussed earlier. Moreover, since the statistic depends only on the attributes of the two actors in a dyad and not on any other ties in the network, it also maintains dyadic independence. That is, the presence or absence of one tie does not influence the probability of others, unless additional structural terms (like triangles or mutual ties) are included in the model.
Thus, including a homophily term allows us to model nodal covariate effects; how actor characteristics affect tie formation—while keeping the model simple and tractable.
Example: Teenage Friends and Lifestyle Study data
For an example including the homophily statistic, we use the the Teenage Friends and Lifestyle Study data called s50 in the networkdata package. The s50 dataset is a subset of 50 girls over a three-year panel study of adolescent friendship networks and health behaviors conducted in a school in the West of Scotland (West and Sweeting 1996). This excerpt was created for illustrative purposes and includes dynamic friendship data over three waves, capturing changes in social ties alongside attributes like gender, sport participation, and substance use. We will focus on the homophily based on smoking behavior.
We only consider cross-sectional network data here so we only focus on the third wave network (we will in later chapters look at modeling longitudinal network data). Let’s prepare the data for the ergm specification. Note that we here instead convert the graph object inot a network one using the package integraph in order to preserve the node attribute of interest
# Load data as graph object from networkdata and extract the third wave network
s50_g <- networkdata::s50[[3]]
# Convert to network object using intergraph
s50_net <- asNetwork(s50_g)
# check netowrk obejct and stored attributes
s50_net Network attributes:
vertices = 50
directed = FALSE
hyper = FALSE
loops = FALSE
multiple = FALSE
bipartite = FALSE
total edges= 77
missing edges= 0
non-missing edges= 77
Vertex attribute names:
smoke vertex.names
No edge attributesWe now test whether students tend to form friendships with others who have the same smoking behavior. The s50 dataset includes a categorical node attribute called smoke, with three levels: non-smoker (1), occasional smoker (2), and regular smoker (3). To test for smoking-based homophily, we fit an ERGM that includes an edge term and a nodematch("smoke") term.
# Fit ERGM with homophily on smoking status
model_smoke <- ergm(s50_net ~ edges + nodematch("smoke"))
summary(model_smoke)Call:
ergm(formula = s50_net ~ edges + nodematch("smoke"))
Maximum Likelihood Results:
Estimate Std. Error MCMC % z value Pr(>|z|)
edges -3.0196 0.1902 0 -15.878 <1e-04 ***
nodematch.smoke 0.5736 0.2425 0 2.365 0.018 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Null Deviance: 1698.2 on 1225 degrees of freedom
Residual Deviance: 569.4 on 1223 degrees of freedom
AIC: 573.4 BIC: 583.6 (Smaller is better. MC Std. Err. = 0)The model includes two terms:
edges: controls for the overall density of the network (should always be included)nodematch("smoke"): counts the number of ties where both nodes have the same smoking status.
This specification assumes that the tendency to form ties is homogeneous across dyads, and the homophily term preserves dyadic independence, as it depends only on the attributes of the two individuals involved in each potential tie.
We interpret the output as follows. The edges term gives the baseline log-odds of a tie between two students, regardless of smoking behavior. The nodematch(“smoke”) term estimates the additional log-odds of a tie when two students share the same smoking status.
Since the coefficient for nodematch("smoke") is positive and significant, we see that students tend to form ties with peers who have similar smoking habits (homophily).
Note on
nodematch()
Note that nodematch("smoke") adds one statistic to the model: the total number of edges connecting nodes that share the same value of the smoke attribute. It does not distinguish between which category is shared, it treats all matches equally. So in our case, it would count:
- Ties between two non-smokers
- Ties between two occasional smokers
- Ties between two regular smokers
All of those contribute to the same term. It does not tell you whether one group is more homophilous than another. If we want more detail, we can instead use nodemix("smoke") as it can separate estimates for each combination of categories (e.g., smoker-smoker, smoker-non-smoker, etc.), that is you get detailed between-group dynamics.
2. Dyadic Dependence: Reciprocity
In ERGMs, we can explicitly model dyadic dependence, that is, the statistical relationship between the presence or absence of ties within pairs of nodes (dyads). This is particularly important in directed networks, where the direction of a tie from node \(u\) to node \(v\) may be statistically related to the reverse tie from \(v\) to \(u\).
To capture this, we include a reciprocity term in the model specification. This term counts the number of mutually connected dyads* i.e., pairs where both \(y_{uv} = 1\) and \(y_{vu} = 1\). Including this term allows the model to account for the observed tendency in many social networks for actors to reciprocate ties—such as returning a favor, replying to a message, or forming a mutual friendship.
An ERGM with both an edge and a reciprocity statistic is specified as:
\(P(G) = \frac{1}{\kappa} \exp\left(\theta_1 \cdot L + \theta_2 \cdot R\right)\)
where \(L = \sum_{u \neq v} y_{uv}\) is the total number of directed ties (edges) and \(R = \sum_{u \neq v} y_{uv} \cdot y_{vu}\).
A positive value for \(\theta_2\) indicates a tendency toward reciprocation, while a negative value suggests an avoidance of mutual ties.
Example: Coleman Friendship
We use the coleman data from earlier to specify an ERGM including reciprocity as statistic.The fitted ERGM includes two terms: a baseline edges term and a mutual term that captures reciprocity (i.e., the tendency for ties to be reciprocated):
# Fit ERGM with reciprocity term
model_rec <- ergm(coleman_mat ~ edges + mutual)
summary(model_rec)Call:
ergm(formula = coleman_mat ~ edges + mutual)
Monte Carlo Maximum Likelihood Results:
Estimate Std. Error MCMC % z value Pr(>|z|)
edges -3.71800 0.09916 0 -37.49 <1e-04 ***
mutual 3.76117 0.23608 0 15.93 <1e-04 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Null Deviance: 7286 on 5256 degrees of freedom
Residual Deviance: 1713 on 5254 degrees of freedom
AIC: 1717 BIC: 1730 (Smaller is better. MC Std. Err. = 1.864)The edge term has a strong negative estimate (\(\hat{\theta}_{\text{edges}} = -3.72\), \(p < 0.0001\)), indicating that ties are generally infrequent in the network. This negative coefficient reflects the baseline log-odds of a directed tie existing between two nodes in the absence of any reciprocation or other structural tendencies.
In contrast, the mutual term has a strong positive estimate (\(\hat{\theta}_{\text{mutual}} = 3.77\), \(p < 0.0001\)), which suggests a highly significant tendency for reciprocated ties. In other words, when a tie exists from node \(u\) to node \(v\), the likelihood that node \(u\) also ties back to node \(v\) is much greater than would be expected by chance, controlling for overall network sparsity.
This combination of results suggests that while directed ties are rare in general, when ties do form, they are very likely to be mutual; a common feature in social networks. Overall, this ERGM confirms that dyadic dependence in the form of reciprocity is a defining feature of the Coleman data network.
3. Markov Dependence: Triangles and Stars
Markov random graphs are a foundational class of models in network statistics, based on the idea that the presence or absence of a tie between two nodes depends only on ties that are “locally adjacent”—specifically, those that share a node. This assumption, known as Markov dependence, implies that edges are conditionally independent unless they share a common node. This implies that the presence or absence of a tie between two nodes may influence other ties in the network, but only if those ties are adjacent. This locality of dependence makes the model tractable while capturing meaningful structural effects.
Formally introduced by Frank and Strauss (1986), Markov random graphs were inspired by analogous models in spatial statistics, e.g., Besag’s auto-logistic models which similarly use local dependencies to define global probability distributions (Besag 1972). The key insight is that network ties can exhibit local dependencies—like clustering or centralization—that can be modeled using well-defined building blocks.
Under Markov dependence, ERGMs are typically specified using edges, \(k\)-stars, and triangle terms, since these configurations reflect dependencies between adjacent ties. Examples of such configurations are shown in Figure 17.1.
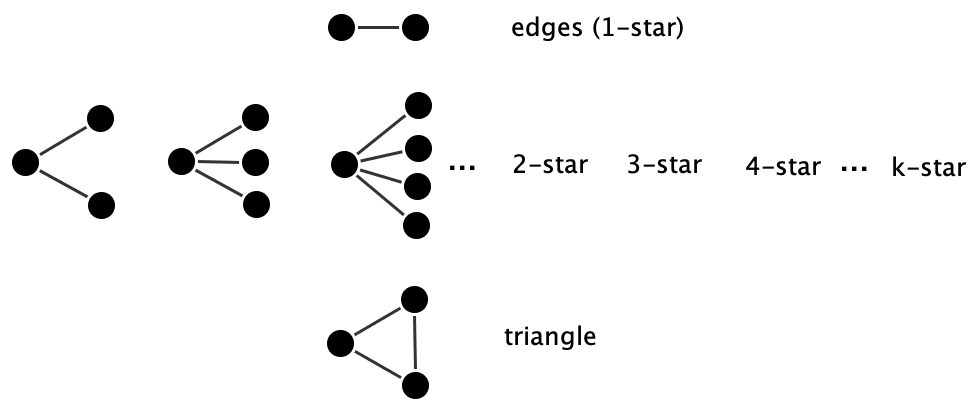
A triangle occurs when three nodes are all pairwise connected. In undirected networks, this represents a basic unit of triadic closure; the idea that “a friend of a friend is likely to become a friend.” In ERGM terms, a triangle statistic is defined as:
\(T = \sum_{u < v < w} y_{uv} \cdot y_{uw} \cdot y_{vw}\)
Including a triangle term in the model allows us to test for transitivity. A positive coefficient on this term suggests a tendency toward forming closed triads, while a negative coefficient implies avoidance of such closure.
In directed networks, we distinguish between:
- Transitive triads: if \(u \to v\) and \(v \to w\), then \(u \to w\)
- Cyclic triads: if \(u \to v\), \(v \to w\), and \(w \to u\)
Each type can be specified as a separate statistic in an ERGM to assess different triadic dynamics.
Star configurations capture the tendency for nodes to have many ties, i.e., to be “popular” or “active” in the network. A \(k\)-star is a configuration where a single node is connected to \(k\) others. The star statistic of order \(k\) is:
\(S_k = \sum_u \sum_{v_1 < \dots < v_k \neq u} y_{uv_1} \cdot \dots \cdot y_{uv_k}\)
Including star terms allows the model to capture degree heterogeneity, reflecting whether some individuals tend to form many more ties than others. Note that in directed networks, we can specify:
- Out-stars (activity): a node sending many ties
- In-stars (popularity): a node receiving many ties
A positive parameter on star terms suggests that nodes with many connections are more likely to gain additional ties—a form of preferential attachment or “rich-get-richer” dynamics.
Example: Florentine Business Network
To illustrate the use of Markov-dependent configurations in ERGMs, we fit a model to the Florentine business network, the classic dataset representing marriage and business ties among Renaissance-era families in Florence. Whie rather small, this undirected network contains important social patterns such as clustering and centralization, making it an ideal candidate for modeling local dependence structures such as edges, stars, and triangles.
The goal of this example is to assess how these network structures contribute to the overall topology of the network using an ERGM based on Markov dependence.
First we visualize the using by loading the data from the networkdata package to obtain it as graph object and to be able to use ggraph:
flob_g <- networkdata::flo_business
class(flob_g) # Confirms it's a 'graph' class object[1] "igraph"flob_p <- ggraph(flob_g, layout = "stress") +
geom_edge_link0(edge_colour = "#666060",
edge_width = 0.8, edge_alpha = 1) +
geom_node_point(fill = "#808080", colour = "#808080",
size = 7, shape = 21, stroke = 0.9) +
theme_graph() +
theme(legend.position = "none") +
ggtitle("Florentine business network")
flob_p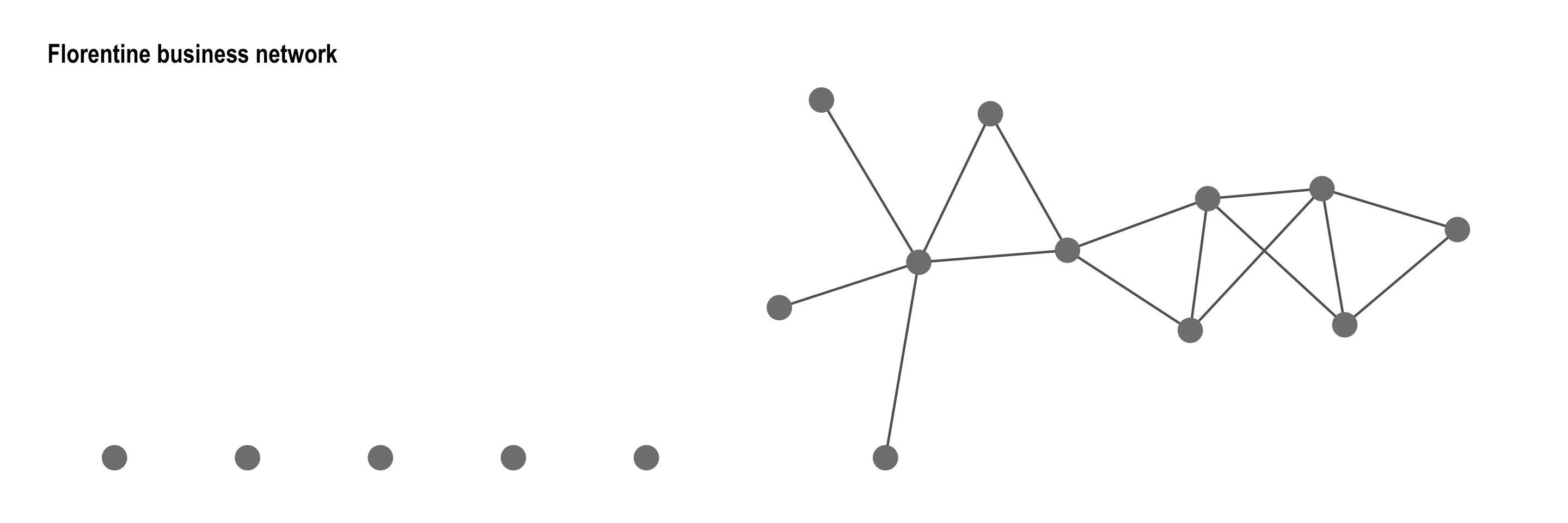
We specify an ERGM including:
edges: to capture baseline tie propensity (density),kstar(2)andkstar(3): to model degree centralization (nodes connected to 2 or 3 others),triangle: to capture triadic closure (transitivity).
The data is loaded from the ergm package and stored as a network class object.
# Load the Florentine business network data
data(florentine)
# The object is a network object representing business ties
flob_net <- flobusiness
class(flob_net) # Confirms it's a 'network' class object[1] "network"# Fit ERGM with Markov dependence terms
set.seed(77)
model_markov <- ergm(flob_net ~ edges + kstar(2) + kstar(3) + triangle)
# Display summary of the model
summary(model_markov)Call:
ergm(formula = flob_net ~ edges + kstar(2) + kstar(3) + triangle)
Monte Carlo Maximum Likelihood Results:
Estimate Std. Error MCMC % z value Pr(>|z|)
edges -4.3454 1.2406 0 -3.503 0.000461 ***
kstar2 1.1257 0.7074 0 1.591 0.111535
kstar3 -0.6467 0.4120 0 -1.570 0.116440
triangle 1.1618 0.6883 0 1.688 0.091416 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Null Deviance: 166.36 on 120 degrees of freedom
Residual Deviance: 79.49 on 116 degrees of freedom
AIC: 87.49 BIC: 98.64 (Smaller is better. MC Std. Err. = 0.2036)The model output provides coefficients for each configuration:
edges: Significantly negative indicating that ties are relatively sparse overall.kstar(2): Not statistically significant suggesting no strong tendency toward moderate centralization (i.e., nodes connected to two others).kstar(3): Also not statistically significant meaning the network does not exhibit a clear preference for or against nodes forming many connections (larger stars).triangle: Significantly positive indicating a strong tendency for triadic closure; that is, if two families are both connected to a third, they are more likely to also be connected to each other.
This suggests the Florentine business network is locally clustered (triadic), but does not support highly centralized hub-like nodes. The network’s structure reflects a preference for mutual interdependence rather than hierarchical dominance.
The good news is that by including triangle and star terms in an ERGM, we can move beyond modeling just dyadic interactions and begin to account for local clustering, degree distributions, and complex relational tendencies. The bad news is that they don’t always work.
While Markov random graph models offer a powerful way to represent local dependence through structures like edges, stars, and triangles, they come with a significant challenge: model degeneracy.
Model degeneracy occurs when an ERGM assigns overwhelming probability to a small set of unrealistic graph configurations—such as the empty graph (no ties) or the complete graph (every possible tie), even though the observed network lies somewhere in between. This typically manifests during estimation as:
- Extremely poor convergence of the MCMC algorithm,
- Implausible simulated networks that look nothing like the observed data,
- A breakdown in model fit across key structural statistics (e.g., triad census, degree distribution).
For example, when fitting a model to the Florentine business network, a model with edges, stars, and triangles may produce simulated networks that deviate substantially from the observed triad census despite having reasonable parameter estimates. This discrepancy arises because certain parameter combinations (especially involving triangles and high-order stars) can push the model into degenerate territory, where the likelihood surface becomes unstable or flat. Thus, careful diagnostic checks are essential when modeling endogenous network structure implying dyadic dependence. We will cover this in more detail in Section 17.2.2.
The degeneracy problem highlights a key limitation of Markov dependence: not all local dependence assumptions lead to coherent global models. Particularly when clustering is strong, models relying solely on Markov terms (edges, stars, triangles) can become computationally fragile or even mathematically incoherent. In the next section, we will examine how social circuit dependence offers an alternative approach to modeling complex interdependence while mitigating model degeneracy.
17.2.2 Model Estimation
Estimating the parameters of an Exponential Random Graph Model (ERGM) involves finding the parameter vector \(\boldsymbol{\theta}\) that maximizes the likelihood of observing the network \(G_{\text{obs}}\) under the specified model:
\[ \hat{\boldsymbol{\theta}} = \arg\max_{\boldsymbol{\theta}} \, P(G_{\text{obs}} \mid \boldsymbol{\theta}) = \frac{\exp\left( \boldsymbol{\theta}^\top \mathbf{s}(G_{\text{obs}}) \right)}{\kappa(\boldsymbol{\theta})} \]
Here, \(\mathbf{s}(G)\) is a vector of network statistics (e.g., number of edges, mutual ties, triangles), and \(\kappa(\boldsymbol{\theta})\) is a normalizing constant that sums the exponential terms over all possible networks with the same number of nodes:
\[ \kappa(\boldsymbol{\theta}) = \sum_{G'} \exp\left( \boldsymbol{\theta}^\top \mathbf{s}(G') \right) \]
This computation is analytically intractable for all but the smallest networks due to the exponential number of possible configurations.
To overcome this, ERGMs use Markov Chain Monte Carlo Maximum Likelihood Estimation (MCMCMLE). The idea is to simulate many networks from the current estimate of the model and compare their statistics to those of the observed network. The process iteratively updates the parameter estimates so that the simulated statistics converge toward the observed ones.
The estimation process, as implemented in the ergm package, proceeds as follows:
Initial Parameter Estimation (MPLE):
The process begins with a Maximum Pseudo-Likelihood Estimate (MPLE), which provides a fast but approximate estimate of \(\boldsymbol{\theta}\). This serves as the starting point for simulation.MCMC Simulation:
Given the current parameter estimates, networks are simulated from the model using Markov Chain Monte Carlo (MCMC) methods; typically a form of Metropolis-Hastings sampling.Likelihood Approximation and Parameter Updating:
The simulated networks are used to approximate the log-likelihood gradient, which informs updates to \(\boldsymbol{\theta}\). These updates move the model toward parameter values that better reproduce the observed network statistics.Iteration:
Steps 2 and 3 are repeated iteratively. At each round, the model simulates networks, compares the simulated statistics to the observed ones, and updates the parameters. The goal is to minimize the difference between observed and expected statistics under the model.
This process continues until convergence is reached, i.e., when the simulated network statistics closely match those of the observed network and parameter updates stabilize.
Note on Metropolis-Hastings sampling
In the ergm package, the Metropolis–Hastings (MH) algorithm is used for MCMC simulation. It evaluates how a proposed tie change affects the network statistics (e.g., edges, triangles) and adjusts the likelihood ratio accordingly. This makes MH well-suited for models with dyad dependence, where toggling one tie may alter the configuration of multiple others. Specifically, the algorithm works as follows:
- Propose a change to the current network state, typically by randomly toggling a tie (i.e., adding or removing an edge between two nodes).
- Compute an acceptance probability, based on the change in the model’s sufficient statistics and the corresponding change in likelihood.
- Accept or reject the proposed change with that probability, ensuring the Markov chain samples from the correct distribution.
Over many iterations, this process produces a sample of networks from the ERGM’s specified distribution, which is then used for parameter estimation and simulation.
In summary, the simulation-based procedure involves two key steps:
- MCMC Sampling: Generate random networks from the current parameter estimates using a Markov chain.
- Score Updating: Adjust the parameter values to reduce the difference between simulated and observed network statistics.
Because ERGMs rely on MCMC simulation to estimate model parameters, it is important to check whether the estimation process has properly converged. MCMC diagnostics help assess whether the Markov chain has explored the space of possible networks sufficiently and whether the simulated networks reflect a stable distribution. Poor convergence can lead to unreliable parameter estimates and misleading inferences. Key diagnostics include
- trace plots (to check stability of simulated statistics over time)
- autocorrelation plots (to assess dependence between samples)
- and comparisons between observed and simulated statistics.
A well-fitting model should not only reproduce the observed statistics on average but also generate networks with similar variability and structure. Running these diagnostics ensures that conclusions drawn from the model are based on a valid and stable estimation process.
While MCMC diagnostics are useful in general, they are especially critical when estimating dyad-dependent ERGMs; models in which the probability of a tie depends on the presence or absence of other ties in the network. This includes models with terms like triangles, \(k\)-stars, or other structural dependencies. In these cases, the network space becomes highly constrained and interdependent, making it more challenging for the Markov chain to explore effectively. As a result, convergence issues are more common, and MCMC diagnostics play a key role in ensuring that the simulation-based estimation has produced reliable parameter values.
For dyad-independent models (e.g., those using only nodal covariates like homophily), estimation is generally simpler and may not require full MCMC sampling or diagnostics. You can actually think of the dyad-independent ERGM as the mathematically equivalent to a logistic regression model applied to all possible dyads in the network. In fact, the ergm package uses maximum pseudo-likelihood estimation (MPLE) for dyad-independent models, which is logistic regression under the hood.
Model Instability and Degeneracy
While MCMC-based estimation enables flexible ERGM modeling, it also introduces potential pitfalls. In particular, unstable ERGMs can give rise to multi-modal probability distributions over the space of possible networks, where most of the probability mass concentrates on a small and unrealistic subset of configurations.
This phenomenon is known as model degeneracy. A degenerate ERGM assigns near-zero probability to most networks in the model space, and high probability only to extreme graphs, such as the completely empty or fully connected one. Since real social networks rarely resemble either of these extremes, such a distribution indicates a serious modeling failure.
Signs of degeneracy include:
- Simulated networks that are always empty or complete, regardless of the observed data.
- Poor convergence of MCMC chains, or failure to reach a stable equilibrium (stationary distribution).
- Large gaps between observed and simulated statistics, especially for higher-order configurations like triangles.
More technically, MCMC simulation is particularly vulnerable to problems like instability and degeneracy when:
Burn-in period is too short: The burn-in period refers to the initial phase of MCMC sampling during which the Markov chain has not yet stabilized. Early samples may be heavily influenced by the starting values and not representative of the true model distribution. If this phase is too short, those unrepresentative samples may skew the estimation.
Post-burn-in sampling is too sparse: After burn-in, we collect samples intended to represent the stationary distribution of the model. If too few of these post-burn-in samples are collected, or if they are too highly correlated (e.g., due to short MCMC intervals), the resulting estimates may be unreliable or noisy.
The model includes strong dependence terms (e.g., many triangle-based or star-based statistics) without sufficient balancing components such as edge terms or decay-weighted statistics like
gwesp(). These terms can make the network space highly constrained and difficult for the MCMC algorithm to explore effectively.
Running MCMC Diagnostics
After fitting an ERGM, use mcmc.diagnostics() to evaluate whether the MCMC estimation has converged and whether the Markov chain has mixed well. This function provides trace plots, density plots, and numerical summaries for each model parameter:
# MCMC convergence check
mcmc.diagnostics(model)We will consider the diagnostics for the model_sc on the lawyer data set above:
Example: Lawyers Network - Cowork Among Partners
The mcmc.diagnostics() function in the ergm package produces trace plots and density plots for each model parameter, allowing us to evaluate the stability and mixing of the MCMC chain. The daignostics consists of two parts. The first part is a plot:
mcmc.diagnostics(model_sc, which = "plots")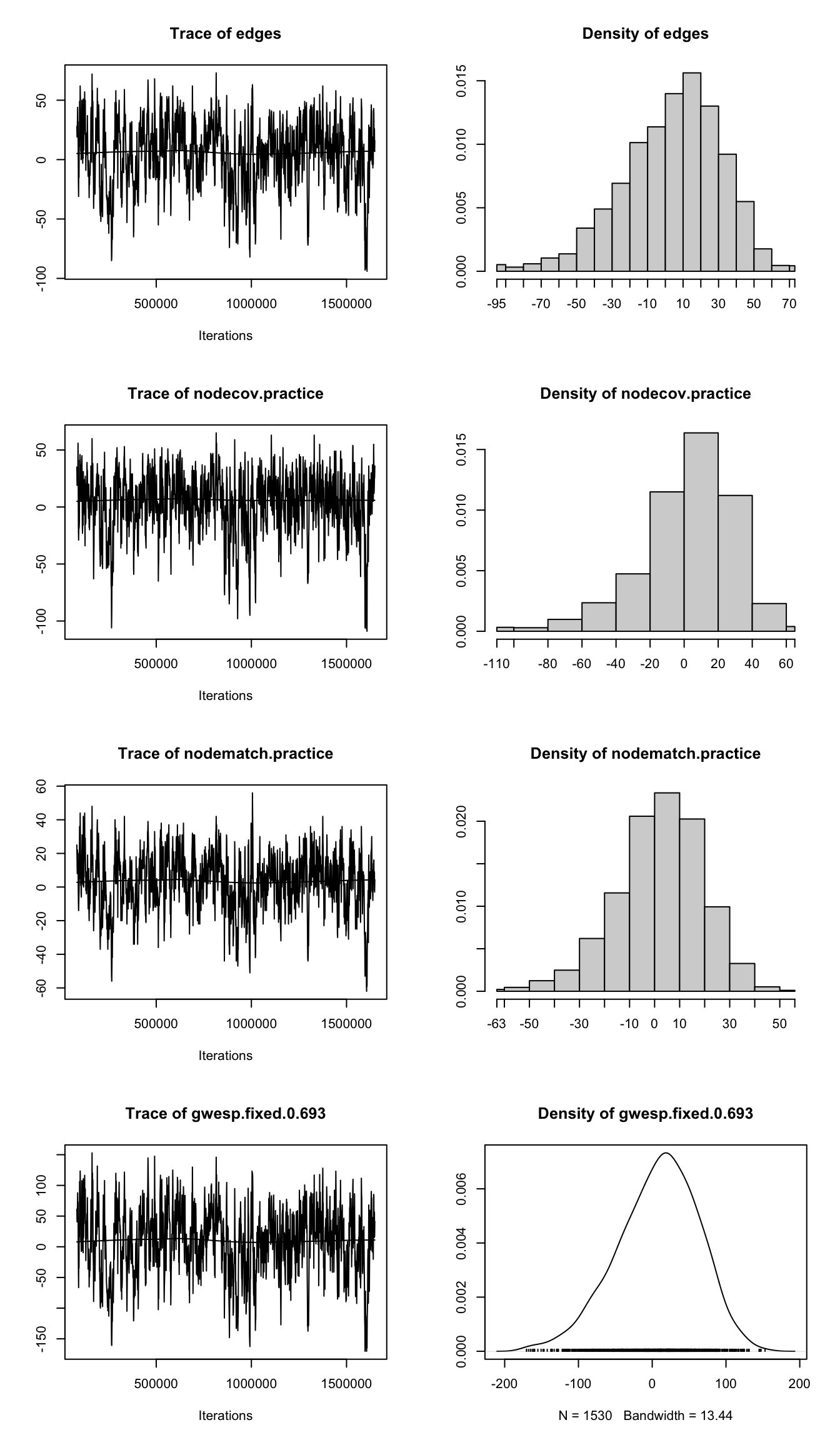
Note: MCMC diagnostics shown here are from the last round of
simulation, prior to computation of final parameter estimates.
Because the final estimates are refinements of those used for this
simulation run, these diagnostics may understate model performance.
To directly assess the performance of the final model on in-model
statistics, please use the GOF command: gof(ergmFitObject,
GOF=~model).The MCMC diagnostic output includes two main types of plots as seen in Figure 17.4: trace plots and density plots, which together help assess whether the Markov chain has properly converged.
The trace plots (left panels of Figure 17.4) display the sampled values of the score function—essentially, the gradient of the log-likelihood—for each model term across the course of the MCMC simulation. In a well-behaved chain, these traces should appear as irregular but stable fluctuations around zero, without discernible trends, drifts, or flat segments. Such patterns indicate good mixing, where the sampler is exploring the parameter space effectively rather than getting stuck.
In the Lazega model, all four trace plots (for edges, nodecov.practice, nodematch.practice, and gwesp.fixed.0.693) exhibit the expected noisy, stable behavior. There are no signs of poor mixing or convergence issues.
The density plots (right panels of Figure 17.4) complement this by summarizing the distribution of the sampled scores for each term. A roughly symmetric, bell-shaped curve centered near zero suggests that the chain has reached its stationary distribution. Here too, all four parameters display smooth, unimodal density curves with means close to zero, providing further evidence that the MCMC sampler has stabilized and that the parameter estimates are reliable.
Together, these visual diagnostics indicate that the model has converged appropriately and that the MCMC estimation procedure has produced a stable and interpretable result.
In addition to the trace and density plots, the mcmc.diagnostics() function provides a set of detailed numerical diagnostics that assess both the stability of the simulated statistics and the convergence behavior of the Markov chain. These diagnostics offer a more granular view of the estimation process and help confirm whether the model has been reliably estimated. We’ll interpret the output in the following.
mcmc.diagnostics(model_sc, which = "texts")Sample statistics summary:
Iterations = 82944:1648640
Thinning interval = 1024
Number of chains = 1
Sample size per chain = 1530
1. Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
edges 4.193 27.69 0.7079 2.030
nodecov.practice 3.084 27.03 0.6911 1.699
nodematch.practice 2.555 17.11 0.4374 1.312
gwesp.fixed.0.693 7.441 54.95 1.4048 3.982
2. Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
edges -58.00 -13.00 7.00 24.00 50.00
nodecov.practice -62.00 -11.75 7.00 22.00 44.77
nodematch.practice -34.77 -7.75 4.00 15.00 32.00
gwesp.fixed.0.693 -112.95 -27.27 11.86 46.56 105.24
Are sample statistics significantly different from observed?
edges nodecov.practice nodematch.practice gwesp.fixed.0.693
diff. 4.193464 3.08431373 2.55490196 7.44060041
test stat. 2.065603 1.81503409 1.94692678 1.86876829
P-val. 0.038866 0.06951867 0.05154351 0.06165506
(Omni)
diff. NA
test stat. 2.018915e+01
P-val. 5.549297e-04
Sample statistics cross-correlations:
edges nodecov.practice nodematch.practice
edges 1.0000000 0.8661702 0.9385818
nodecov.practice 0.8661702 1.0000000 0.8058032
nodematch.practice 0.9385818 0.8058032 1.0000000
gwesp.fixed.0.693 0.9930583 0.8706234 0.9326873
gwesp.fixed.0.693
edges 0.9930583
nodecov.practice 0.8706234
nodematch.practice 0.9326873
gwesp.fixed.0.693 1.0000000
Sample statistics auto-correlation:
Chain 1
edges nodecov.practice nodematch.practice gwesp.fixed.0.693
Lag 0 1.0000000 1.0000000 1.0000000 1.0000000
Lag 1024 0.7830828 0.6976898 0.7312736 0.7512523
Lag 2048 0.6230787 0.5053844 0.5691328 0.5927850
Lag 3072 0.5060997 0.3787281 0.4569260 0.4783505
Lag 4096 0.4117891 0.3017643 0.3746105 0.3901042
Lag 5120 0.3397918 0.2345665 0.3080189 0.3204952
Sample statistics burn-in diagnostic (Geweke):
Chain 1
Fraction in 1st window = 0.1
Fraction in 2nd window = 0.5
edges nodecov.practice nodematch.practice gwesp.fixed.0.693
1.183854 1.102967 1.430812 1.202088
Individual P-values (lower = worse):
edges nodecov.practice nodematch.practice gwesp.fixed.0.693
0.2364708 0.2700415 0.1524842 0.2293296
Joint P-value (lower = worse): 0.646062
Note: MCMC diagnostics shown here are from the last round of
simulation, prior to computation of final parameter estimates.
Because the final estimates are refinements of those used for this
simulation run, these diagnostics may understate model performance.
To directly assess the performance of the final model on in-model
statistics, please use the GOF command: gof(ergmFitObject,
GOF=~model).One key output compares the mean of the simulated statistics to the corresponding observed values. For most terms, including nodecov.practice, nodematch.practice, and the gwesp statistic—there is no significant difference between simulated and observed statistics, indicating a good model fit. The only exception is the edges term, which shows a small but statistically significant deviation (\(p\) = 0.0389). This suggests a slight misfit on overall tie density, though the magnitude of the difference is modest and not cause for concern.
The cross-correlations between simulated statistics are moderately high but consistent with the expected dependencies among model terms. For example, ties that contribute to homophily (nodematch.practice) also increase the total number of edges, leading to a natural correlation. None of the observed correlations approach levels (e.g., > 0.95) that would indicate redundancy or raise concerns about model identifiability or degeneracy.
Looking at auto-correlation, we see that values for all parameters decay steadily with increasing lags. This pattern is typical of a well-mixing MCMC chain and indicates that the sampler is not highly autocorrelated, which would reduce efficiency.
Finally, the Geweke burn-in diagnostic compares the means of the early and late segments of the MCMC chain. All terms yield non-significant \(p\)-values (ranging from 0.15 to 0.27), suggesting that the Markov chain has likely reached stationarity. The joint \(p\)-value of 0.64 further supports this conclusion.
Taken together, these diagnostics confirm that the MCMC estimation for the ERGM is well-behaved. The parameter estimates appear stable, the chain has mixed adequately, and the model reproduces key features of the observed network. While the slight misfit on the edges term is noted, it does not compromise the validity of the overall model, which can be interpreted with confidence.
As noted, MCMC requires more care and feeding, meaning users often need to tune control parameters, assess diagnostics, and sometimes revise the model specification to ensure convergence and realism. Practically, this may involve:
- Increasing
MCMC.burninandMCMC.samplesizeincontrol.ergm(), - Replacing raw triangle or star terms with smoother alternatives (e.g.,
gwesp()orgwdsp()), - Simplifying the model to reduce overfitting or internal tension among terms.
Note on MCMC control parameters
Control parameters for the MCMC algorithm can be found here help(control.ergm)
For a detailed technical treatment of model instability in ERGMs, see Schweinberger (2011). Alternative specification strategies that improve stability are discussed in Snijders et al. (2006), while the formulation and rationale behind the gwesp term, and curved exponential family models more broadly, are addressed in Hunter and Handcock (2006).
17.2.3 Model Fit
After confirming that the MCMC estimation has converged properly (as diagnosed through trace plots, numerical summaries, and Geweke statistics) the next essential step is to assess the fit of the model to the observed network.
While MCMC diagnostics ensure that parameter estimates are stable and reliable, they do not tell us whether the model is substantively adequate, that is, whether it captures the essential structure of the network. For this, we turn to goodness-of-fit (GOF) diagnostics.
There are two complementary questions in ERGM model checking:
Did the model reproduce the terms included in the formula?
This is effectively ensured by the maximum likelihood estimation procedure. If convergence has been achieved, the model will reproduce the sufficient statistics (e.g., number of edges, triangles) used in the specification.Does the model reproduce broader structural properties of the network?
This is the more important and revealing test. GOF checks compare simulated networks to the observed one on key network features not explicitly included in the model. These typically include:- Degree distribution (node-level centrality)
- Edgewise shared partners (ESP) (local clustering)
- Geodesic distances (overall reachability)
This second category helps detect model misspecification, i.e., features of the network that the model fails to account for.
Running Goodness-of-Fit Checks in ERGM
The ergm package provides the gof() function, which performs a simulation-based goodness-of-fit assessment. This function compares the observed network to a distribution of networks simulated from the fitted model, focusing on structural features not directly modeled.
The typical workflow is:
# Run GOF assessment
gof_model <- gof(model)
# View numeric summary
summary(gof_model)
# Plot GOF results
plot(gof_model)Example: Lawyers Network - Cowork Among Partners
We now assess the fit of the ERGM specified for Lazega’s co-working network, which included:
edges: baseline tie probability,nodecov("practice"): effect of practice area on tie activity,nodematch("practice"): homophily within practice areas,gwesp(0.693, fixed = TRUE): transitive closure (triadic clustering).
The goal is to evaluate whether the model, beyond reproducing the modeled statistics, also captures broader structural features of the observed network.
We use the gof() function from the ergm package to simulate networks under the fitted model and compare them to the observed network on several unmodeled statistics:
gof_sc <- gof(model_sc, plotlogodds=TRUE) # this will produce 4 plots
par(mfrow = c(2, 2)) # figure orientation with 2 rows and 2 columns
plot(gof_sc)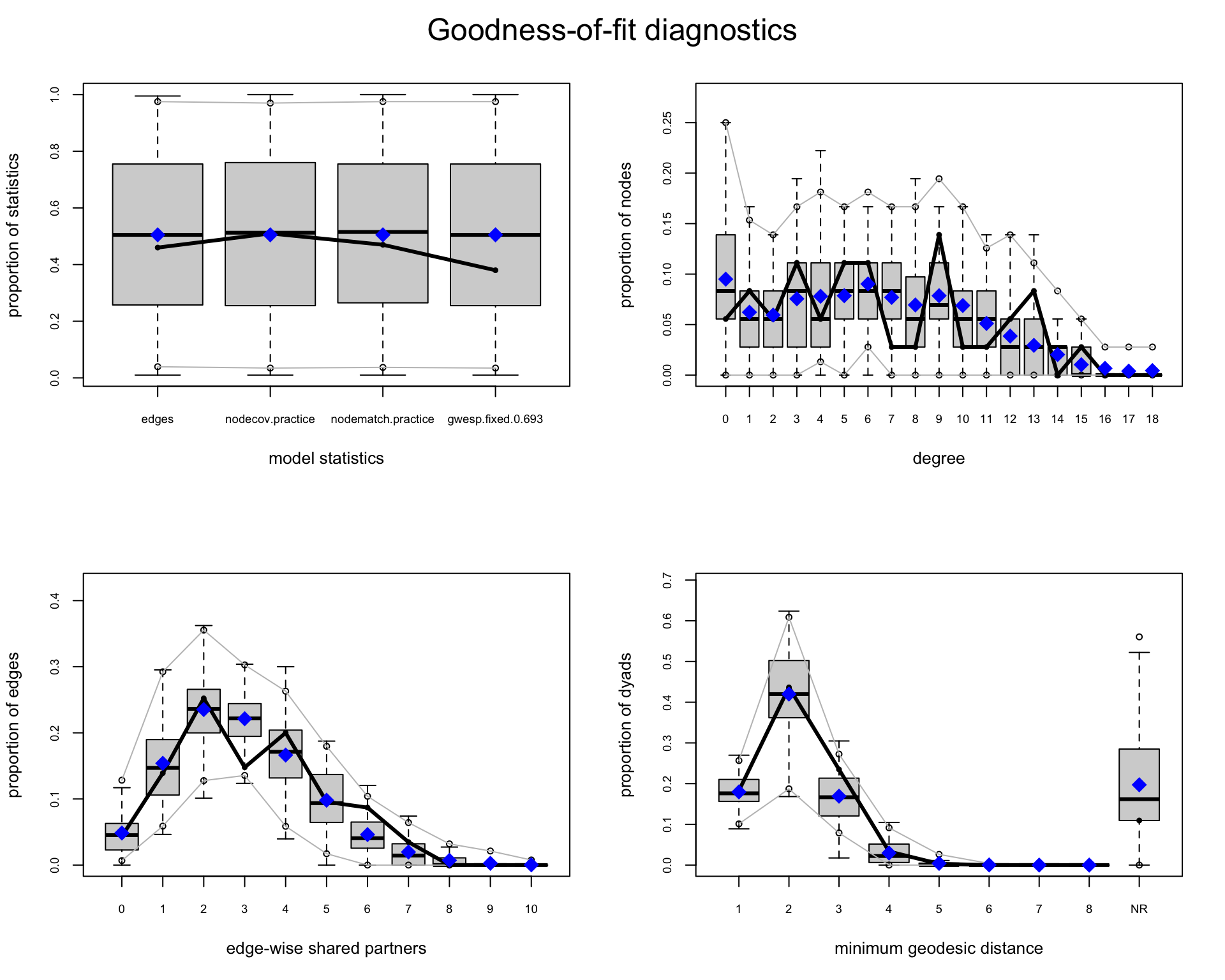
Interpreting th GOF plots
In the GOF plots generated by the ergm package, the meaning of the black line and blue diamond differs slightly depending on the panel:
- Model statistics plot:
- Blue diamond: The observed value of each modeled statistic in the empirical network.
- Black line: The mean value of that statistic across the simulated networks.
- Other GOF plots (e.g., degree, geodesic distance, ESP):
- Black line: The observed distribution of the statistic (e.g., degree counts) in the empirical network.
- Blue diamonds: The mean of the simulated distributions at each value or bin.
Good model fit is indicated when the black line lies within the range of the simulated distributions (shown as boxplots or shaded areas), and aligns closely with the blue diamonds.
This goodness-of-fit check produces plots for several structural features, including both modeled and un-modeled terms. The GOF plots in Figure 17.5 compare statistics from the observed network (black lines or blue diamonds) to distributions of the same statistics across networks simulated from the model:
- Model statistics: the sufficient statistics explicitly specified in the model formula (e.g.,
edges,nodematch,gwesp). This plot shows whether the model reproduces the statistics it was explicitly fit to match. Each boxplot represents the distribution of simulated values for a modeled term (e.g.,edges,nodematch.practice,gwesp), and the blue diamond marks the observed value. Good fit is indicated when the diamond lies near the center of the box. This panel essentially checks if maximum likelihood estimation succeeded. - Degree distribution: the number of ties per node. The model accurately captures the variability in the number of ties per node if the observed degree frequencies fall within the simulated distribution at most points.
- Geodesic distances: shortest paths between nodes. If the model reflects the observed network’s overall connectivity, the distribution of shortest path lengths should align closely with those from the simulations.
- Edgewise shared partners (ESP): the number of common neighbors shared by directly connected pairs of nodes. This panel can typically indicate clustering tendencies. Note that ESP should not be interpreted as a fit criterion in the example shown in Figure 17.5, since it is directly modeled via the
gwespterm. Including it in GOF checks may simply reflect that the model was designed to reproduce it.
Note on using log-odds instead
Normally, GOF plots show the proportion (e.g., of nodes with a given degree) on the y-axis. Using the following and setting plotlogodds = TRUE transforms those proportions to log-odds:
\[
\text{log-odds}(p) = \log\left(\frac{p}{1 - p}\right)
\] In other words, you instead run gof(model, plotlogodds=TRUE).
This is useful when you’re interested in small differences in low-probability bins (e.g., rare degrees or long geodesic distances). Values close to 0 (e.g., rare degrees or high distances) are spread out and more visible. Differences between observed and simulated values in the tails become more pronounced. Plots become less intuitive if you’re unfamiliar with log-odds, so interpret with care.
In addition to the plots shown in Figure 17.5, we can also look at the printed GOF summary:
gof_sc
Goodness-of-fit for degree
obs min mean max MC p-value
degree0 2 0 3.42 10 0.90
degree1 3 0 2.24 8 0.74
degree2 2 0 2.14 8 1.00
degree3 4 0 2.72 7 0.66
degree4 2 0 2.81 8 1.00
degree5 4 0 2.83 7 0.60
degree6 4 0 3.25 7 0.88
degree7 1 0 2.77 7 0.34
degree8 1 0 2.50 8 0.64
degree9 5 0 2.83 9 0.34
degree10 1 0 2.48 9 0.62
degree11 1 0 1.84 5 0.92
degree12 2 0 1.39 6 0.70
degree13 3 0 1.06 5 0.20
degree14 0 0 0.73 4 0.98
degree15 1 0 0.37 3 0.58
degree16 0 0 0.24 2 1.00
degree17 0 0 0.14 3 1.00
degree18 0 0 0.16 2 1.00
degree19 0 0 0.04 1 1.00
degree20 0 0 0.02 1 1.00
degree21 0 0 0.02 1 1.00
Goodness-of-fit for edgewise shared partner
obs min mean max MC p-value
esp0 5 0 4.86 11 1.00
esp1 16 6 16.27 31 0.98
esp2 29 8 26.01 44 0.62
esp3 17 8 25.21 41 0.28
esp4 23 4 19.69 51 0.74
esp5 11 0 11.76 27 1.00
esp6 10 0 5.62 20 0.38
esp7 4 0 2.47 10 0.56
esp8 0 0 0.87 7 1.00
esp9 0 0 0.33 3 1.00
esp10 0 0 0.04 1 1.00
esp11 0 0 0.04 1 1.00
esp12 0 0 0.02 1 1.00
Goodness-of-fit for minimum geodesic distance
obs min mean max MC p-value
1 115 56 113.19 170 0.92
2 275 106 264.57 393 0.92
3 148 11 106.60 192 0.26
4 21 0 18.60 66 0.76
5 2 0 2.61 19 0.62
6 0 0 0.21 5 1.00
7 0 0 0.01 1 1.00
Inf 69 0 124.21 434 0.84
Goodness-of-fit for model statistics
obs min mean max MC p-value
edges 115.0000 56.00000 113.1900 170.0000 0.92
nodecov.practice 129.0000 74.00000 130.0500 174.0000 1.00
nodematch.practice 72.0000 40.00000 70.8400 119.0000 0.94
gwesp.fixed.0.693 181.2969 69.40236 177.6489 291.4062 0.76The numerical output provides a detailed assessment of how well the fitted ERGM reproduces both the modeled terms and modeled structural features of the observed network.
The degree distribution is well captured across nearly all values, with observed counts generally falling within the range of those generated by simulations. Most Monte Carlo \(p\)-values are high (e.g., > 0.5), indicating no significant deviation between the observed and simulated degree frequencies.
Minimum geodesic distances, a measure of global connectivity, show reasonable agreement between observed and simulated networks. While the fit is slightly weaker at a geodesic distance of 3 (\(p = 0.08\)), all other distances are well within acceptable bounds, suggesting that the model captures the overall reachability structure effectively.
Lastly, the model terms explicitly included in the formula (edges, nodecov.practice, nodematch.practice, and gwesp) are all closely matched by the simulated networks, with very high \(p\)-values across the board. This confirms that the maximum likelihood estimation successfully reproduced the sufficient statistics.
These diagnostics together indicate that the model performs well. It reproduces the modeled terms accurately, and also generalizes to capture broader structural features such as degree variation and path lengths. Since the model has also passed MCMC convergence diagnostics, we can conclude that the ERGM is both well-estimated and substantively valid in representing the network-generating processes in the Lazega law firm.
4. Social Circuit Dependence: GWESP
In response to the degeneracy issues inherent in classic Markov ERGMs, researchers have proposed alternative specifications that build more stable dependence structures into the model. One promising approach is based on social circuit dependence Snijders et al. (2006).
Social circuit dependence modifies the way tie dependencies are specified in the model. Instead of assuming that two ties are conditionally dependent simply because they share a node (as in Markov dependence), social circuit dependence restricts dependence to occur only when two ties would complete a 4-cycle in the network. Under social circuit dependence, network ties are assumed to self-organize through 4-cycles, i.e., closed paths involving four distinct nodes. Two potential ties are considered conditionally dependent only if they would complete a 4-cycle in the network. In other words, the existence of a tie between \((u, v)\) is only dependent on a tie between \((w, z)\) if adding both would close such a circuit.
Examples of configurations based on this depdence assumption are shown in Figure 17.2.
This more constrained form of local dependence avoids the pitfalls of degeneracy by reducing the likelihood that the model overemphasizes clustering or centralization. It reflects more realistic assumptions about how social ties form: not purely through dyadic exchange or triadic closure, but through broader patterns of interconnection.
The Geometrically Weighted Edgewise Shared Partner (GWESP) statistic is a commonly used term in ERGMs to capture triadic closure, the tendency for connected nodes to have shared partners, as sown in Figure 17.3. Unlike a simple triangle count, GWESP down-weights the contribution of additional shared partners to help prevent model degeneracy and improve stability.
To formalize this, we let:
Then the GWESP statistic is defined as:
\[ \text{GWESP}(G; \alpha) = \sum_{u < v} y_{uv} \cdot \left(1 - (1 - e^{-\alpha})^{p_{uv}} \right) \]
When \(\alpha\) is close to zero, the statistic approaches a simple count of edges with at least one shared partner. When \(\alpha\) is larger, the contribution of each additional shared partner is increasingly discounted.
GWESP provides a smooth and stable way to model transitivity in networks. It is often used in place of triangle counts to reduce the risk of model degeneracy; where the model produces unrealistic networks concentrated on extremes (e.g., empty or complete graphs).
In practice, GWESP is typically included in ERGMs with a fixed decay value using the
gwesp()term inergm::ergm().A commonly used value for \(\alpha\) is 0.693, which is approximately \(\log(2)\). This choice has a convenient and interpretable consequence: With \(\alpha = \log(2)\), each additional shared partner contributes about half as much as the one before. For example, the first shared partner contributes ~50% of the max possible increment, the second adds ~25%, the third adds ~12.5%, and so on. This exponential discounting reflects a realistic assumption: having one or two mutual friends greatly increases the chance of tie formation, but the influence of additional mutual friends diminishes quickly.
In some models, it may be beneficial to fix \(\alpha\) to a value based on theory or prior experience (common in applied work), or estimate \(\alpha\) directly from the data (
fixed = FALSEingwesp()), though this can lead to convergence issues or overfitting. In practice, usinggwesp(0.693, fixed = TRUE)is often a safe and interpretable starting point.Next we demonstrate how to fit an ERGM using GWESP and interpret the results.
Example: Lawyers Network - Cowork Among Partners
To demonstrate how ERGMs capture social circuit dependence, we will use the same subset of this network as earlier: we want to check whether or not the partners of the firm more frequently work together with other partners having the same practice, whilst also including a statistic related to triadic clustering. We import the data as a graph object from the
networkdatapackage:We then create an adjacency matrix from the directed graph for the first 36 lawyers in the network corresponding to the partners of the firm (see attribute ‘status’). Note that we this time create the network object ourselves from the symmetrized adjacency matrix.
This example includes the following statistics:
edges: baseline tie probability,nodecov("practice"): effect of practice area on tie activity,nodematch("practice"): homophily within practice areas,gwesp(0.693, fixed = TRUE): transitive closure (triadic clustering).nodecov("...")The
nodecov("...")term in an ERGM includes a node-level covariate effect, where the probability of forming a tie is modeled as a function of the attribute value for each node. Specifically, for an undirected network, it sums the attribute values of both nodes involved in each dyad. A positive coefficient indicates that nodes with higher values on the given attribute are more active in forming ties (i.e., they tend to have higher degree). If you’re modeling a binary categorical attribute (e.g., practice = 0 or 1), then the statistic tests whether being in group 1 (e.g., corporate practice) increases a lawyer’s general tendency to form ties, regardless of whom they connect with.These reflect both attribute-based processes and structural dependencies consistent with social circuit theory.A positive and significant `gwesp coefficient would support the idea of social circuit dependence, where ties are not just formed dyadically or through attributes, but also through embedded collaboration patterns within the firm’s structure.
The code below creates the co-work network object for the 36 partners, adds the practice attribute as a binary variable and fits the ERGM with the above defined statistics:
Let’s interpret the output: The fitted model includes four terms:
edges,nodecov("practice"),nodematch("practice"), andgwesp(0.693, fixed = TRUE). Each coefficient represents the log-odds change in the probability of a tie associated with that network statistic, controlling for the others. What do these estimates tell us?edges(\(\hat\theta = -4.41\), p < 0.001): Ties are rare overall; the network is sparse.nodecov("practice")(\(\hat\theta = 0.18\), p < 0.05): Lawyers from a given practice area (e.g., corporate) are slightly more likely to form ties overall.nodematch("practice")(\(\hat\theta = 0.61\), p < 0.001): Strong evidence of homophily, lawyers are significantly more likely to collaborate within their own practice area.gwesp(0.693)(\(\hat\theta = 1.15\), p < 0.001): High and significant triadic closure effect, indicating a strong tendency for collaboration among those with shared partners—consistent with social circuit dependence.Taken together, the results indicate that processes of attribute-related activity, assortative mixing by attribute (homophily), and structural closure (via triadic dependence) operate concurrently in shaping tie formation within the Lazega co-working network.